This is all about priority queue problems with using different techniques for storing the data in a queue, the priority queue could be similar to a queue in a hospital ER ward where the people with the biggest of problems are treated first. I am finding all of the computer science course at Stanford really interesting.
But a heap implementation is similar to a binary tree where the top node is the lowest value and the further you go down each part of the tree you will find higher and higher values. As you can see the below picture, but the main thing is that the highest values may be associated on another place compared to the next highest value, but when you remove the minimum value then you place the last node from the tree to the top node and then move that down to where it should be.
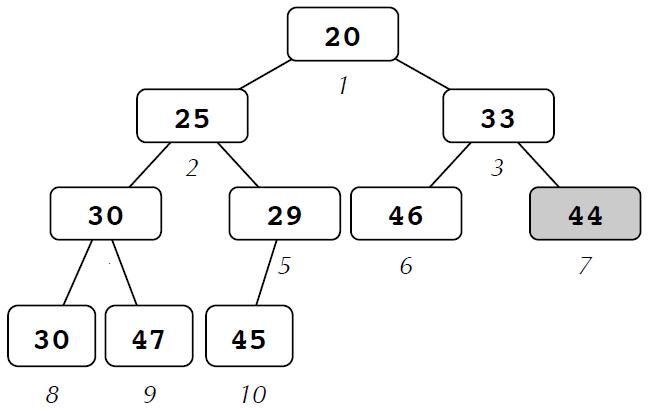
So to insert the values, I am using a recursive funciton
void PQueue::insertValue(int heapInsert) { int newElemI = heapInsert; // need to find out if the parent value if (heapInsert > 0) { // decrement the heapInsert since we start from 0. heapInsert--; // if we are at the top then make it check with the top if (heapInsert == 1) heapInsert=0; else // else goto the parent node heapInsert/=2; // if parent node is greater than the present node, then swap and go up if (heapValues[(heapInsert)] > heapValues[newElemI]) { // swap values swapValues((heapInsert), newElemI); return insertValue(heapInsert); } } return; } |
where it will call itself if a swap happens e.g the parent node is higher in value than the present node that we are checking, and the way that it works out the parent node is to divide the heapInsert by 2, but of course the top 3 nodes that is a special condition and also since arrays start from 0, then we have to — (-1) from the heapinsert value to start with. The newElemI is where we are at present.
To remove the top element, we need to remove that element and replace with the last node from the array, but then move this value down into the tree depending on if the value is less higher than the lowest value beneath it, so once again I did a recursive method that will call itself if a swap occurs, we just need to test the lower left/right elements first to find the lowest value and then check against that with the parent value and if so, swap.
void PQueue::moveRootDown(int rootID) { // test to see which one of the lower two are the smallest of values int leftValue = (rootID*2); int rightValue = (rootID*2)+1; int smallest =-1; if (leftValue <= heapUsedSize) smallest = leftValue; if (rightValue <= heapUsedSize) if (heapValues[smallest-1] > heapValues[rightValue-1]) smallest = rightValue; if (smallest == -1) return; if (heapValues[rootID-1] > heapValues[smallest-1]) { swapValues(rootID-1, smallest-1); moveRootDown(smallest); } } |
that was the main aspects again of the assignment and here is the full source code, I have included the source code and the assignment PDF file in the zip file attached
#include "pqueue.h" #include "genlib.h" #include <iostream> /* heap implementation */ const int heapStart = 10; PQueue::PQueue() { heapSize = heapStart; heapValues = new int[heapStart]; heapUsedSize = 0; } PQueue::~PQueue() { delete[] heapValues; } bool PQueue::isEmpty() { if (heapUsedSize == 0) return true; else return false; } int PQueue::size() { return heapUsedSize; } void PQueue::add(int newElem) { // if we are the max then double if (heapSize == heapUsedSize) doubleCapacity(); heapValues[heapUsedSize] = newElem; insertValue(heapUsedSize); heapUsedSize++; } // newElemI = index value of the new insert void PQueue::insertValue(int heapInsert) { int newElemI = heapInsert; // need to find out if the parent value if (heapInsert > 0) { // decrement the heapInsert since we start from 0. heapInsert--; // if we are at the top then make it check with the top if (heapInsert == 1) heapInsert=0; else // else goto the parent node heapInsert/=2; // if parent node is greater than the present node, then swap and go up if (heapValues[(heapInsert)] > heapValues[newElemI]) { // swap values swapValues((heapInsert), newElemI); return insertValue(heapInsert); } } return; } void PQueue::swapValues(int swap1, int swap2) { int tmp = heapValues[swap1]; heapValues[swap1] = heapValues[swap2]; heapValues[swap2] = tmp; } void PQueue::printOut() { for (int i =0; i < heapUsedSize; i++) cout << "i " << i << " " << heapValues[i] << endl; } // double the capacity of the heap size void PQueue::doubleCapacity() { int *temp = new int[heapSize*2]; for (int i =0; i < heapSize; i++) temp[i] = heapValues[i]; delete[] heapValues; heapValues = temp; heapSize *=2; } int PQueue::extractMin() { if (isEmpty()) Error("no more values"); else { int returnValue = heapValues[0]; heapUsedSize--; heapValues[0] = heapValues[heapUsedSize]; moveRootDown(1); return returnValue; } return 0; } void PQueue::moveRootDown(int rootID) { // test to see which one of the lower two are the smallest of values int leftValue = (rootID*2); int rightValue = (rootID*2)+1; int smallest =-1; if (leftValue <= heapUsedSize) smallest = leftValue; if (rightValue <= heapUsedSize) if (heapValues[smallest-1] > heapValues[rightValue-1]) smallest = rightValue; if (smallest == -1) return; if (heapValues[rootID-1] > heapValues[smallest-1]) { swapValues(rootID-1, smallest-1); moveRootDown(smallest); } } |
here is what I added to the header file for the private aspects of the class.
// heap size = the total amount of size // heap used size = the amount of used space in the heap size // heap values = the actual values within the heap int heapSize, heapUsedSize; int *heapValues; void doubleCapacity(); void printOut(); void insertValue(int heapInsert); void swapValues(int swap1, int swap2); void moveRootDown(int rootID); |
